MATEMATICAS

MATEMATICAS

2 de Febrero

Realizamos los siguientes ejercicios en el cuaderno de matemáticas y solucionamos.

9 de febrero

16 de febrero

Vamos a tomar apuntes de las dos páginas en el cuaderno y desarrollamos.

23 de febrero

Tomar apuntes en el cuaderno de matemáticas y realizar los ejercicios.

EJEMPLOS: 4 + 8 = 8 + 4

12 = 12

(2+3) + 5 = 2 + (3 + 5)

5 + 5 = 2 + 8

10 = 10

2 de Marzo

Prestar atención a las explicaciones que da la docente referente al tema de las propiedades de la adición o suma.

Luego escribir en el cuaderno la siguiente actividad y desarrollar.

La sustracción: para restar dos números se coloca el sustraendo debajo del minuendo y se restan de derecha a izquierda las cifras correspondientes.

Se utilizan dos escrituras para representar la sustracción horizontal y vertical.

9 de Marzo

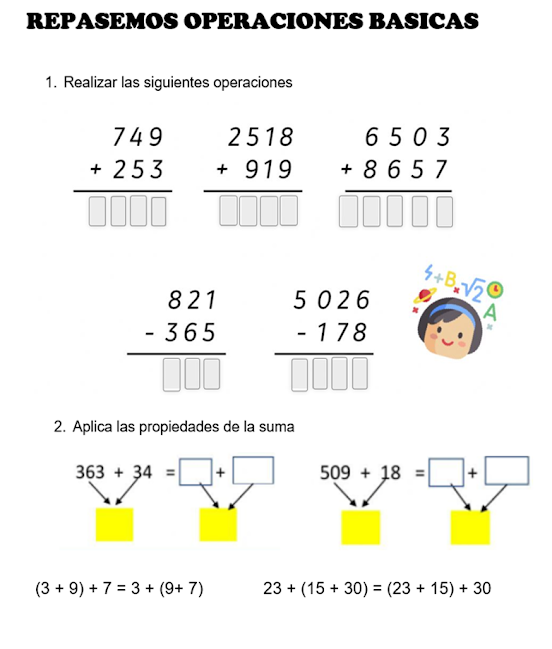
ACTIVIDAD

1. Resuelve, recorta y arma el rompecabezas según los resultados obtenidos.

2. Resuelve las restas y colorea el dibujo de acuerdo con las claves de las respuestas.

16 de Marzo

LA MULTIPLICACION:

Es la suma de sumandos iguales. Los términos de la multiplicación son los factores y el producto.

PROPIEDADES DE LA MULTIPLICACIÓN

PROPIEDAD CONMUTATIVA: En una multiplicación se puede cambiar el orden de los factores y se obtiene el mismo producto.

6x4 = 4x6

24 24

PROPIEDAD ASOCIATIVA: En una multiplicación de 3 factores, los factores se pueden asociar de diferentes formas y se obtiene el mismo producto

(4x2) x 8=4x(2x8)

8 x 8 = 4x16

64 = 64

PROPIEDAD DISTRIBUTIVA: Se relaciona la multiplicación con la adición o la sustracción.

(2 + 7 ) X 5 ( 2 + 7 ) X 5 = 2 X 5 + 7 X 5

10 + 35

9 X 5 45

Aplica la propiedad distributiva

Primera forma

PROPIEDAD MODULATIVA: Al multiplicar un numero natural por 1 no se altera la cantidad, si el orden de los factores se cambia el producto sigue igual.

3x4=12 4x3=12

19 de Marzo

6 de Abril

LA DIVISIÓN

Dividir es repartir una cantidad en partes iguales.

Términos de la división

DIVIDENDO: Cantidad que se reparte

DIVISOR: Número de partes iguales que se sacan del dividendo.

COCIENTE: Cantidad que le pertenece a cada uno de los integrantes del divisor.

RESIDUO: Es la cantidad que va sobrando durante el proceso de la división

13 de Abril

PROBLEMAS DE DIVISION

1. ¿Cuántos murales, con 5 postales de plantas cada uno, se pueden formar? ¿Cuántas postales sobran?

2. ¿Cuántos murales con 7 postales de animales cada uno se pueden formar? ¿Cuántas postales sobran?

3. En la librería hay 256 libros para repartir en 4 cajas. ¿Cuántos libros hay por caja?

4. María compró 256 stickers para repartirlos entre sus 8 amigos y ella. ¿Cuántos stickers le toca a cada uno?

5. Realiza las siguientes divisiones en el cuaderno. Encierra con color amarillo las que sean exactas.

Vamos a aprender a dividir por 2 cifras.

23 de Abril

DIVISIONES POR DOS CIFRAS

Ahora vamos a practicar.

27 de abril

MULTIPLOS

El conjunto de múltiplos de un numero está formado por todos los resultados de la tabla de multiplicar del número, los múltiplos de un número son infinitos. El cero es múltiplo de todos los números.

4 de Mayo

2. Completa los espacios:

24 es múltiplo de 3 porque 3 X _______ = 24

75 es múltiplo de 5 porque 5 X _______ = 75

14 es múltiplo de 7 porque 7 X _______ = ______

70 es múltiplo de 2 porque _______ X _______ = 70

3. Elige la respuesta correcta:

Indica si los siguientes números son múltiplos de 3, de 7 o de 10:

14,21,28,35,42: son múltiplos de _______

6,9,12, 15,18: son múltiplos de _______

30, 40, 50, 60: son múltiplos de _______

4. Encierra los productos de la tabla multiplicando según la clave:

° En color verde los productos de la tabla de multiplicar del 2

° En color rojo los productos de la tabla de multiplicar del 3

° En color azul los productos de la tabla de multiplicar del 4

° En color amarillo los productos de la tabla de multiplicar del 5

° En color café los productos de la tabla de multiplicar del 6

Ten en cuenta que algunos productos los deben encerrar más veces.

5. Unir el número con sus múltiplos.

25 de Mayo

Mínimo común múltiplo

El mínimo común múltiplo (mcm) de dos números es el menor de los múltiplos comunes entre dos números. El mcm debe ser mayor que cero.

Múltiplo

Los múltiplos de un número son los que obtienes cuando lo multiplicas por otros números.

Vamos a ver un ejemplo de los múltiplos de 2 y de 3. Para calcular sus múltiplos hay que ir multiplicando el 2 y el 3 por 1, por 2, por 3, etc.

2 x 1 = 2

2 x 2 = 4

2 x 3 = 6

2 x 4 = 8

y así sucesivamente hasta infinitos números.

3 x 1 = 3

3 x 2 = 6

3 x 3 = 9

3 x 4 = 12

y así sucesivamente hasta infinitos números.

mínimo común múltiplo

Múltiplo Común

Un múltiplo común es un número que es múltiplo a la vez de dos o más números, es decir, es un múltiplo común a esos números.

mínimo común múltiplo

Habrá que ver qué múltiplos tienen en común el dos y el tres, que en la imagen figuran en verde, es decir, el 6, el 12 y el 18. Hay que tener en cuenta que los múltiplos son infinitos y que nosotros solo hemos mostrados los primeros de cada número.

Mínimo común múltiplo

El mínimo común múltiplo es el número más pequeño de los múltiplos comunes.

Siguiendo con el ejemplo anterior, si los múltiplos comunes de 2 y de 3 eran 6, 12 y 18, el mínimo común múltiplo o mcm es 6, ya que es el menor de los múltiplos comunes.

1 de Junio

DIVISORES DE UN NUMERO

Los divisores de un número son las cantidades que al hacer reparticiones generan grupos exactos de elementos. Es decir que cuando se dividen las cantidades obtengo residuo cero. El 1 es divisor de todos los números. Analiza el ejemplo de los divisores de cuatro:

De esta manera se puede Observar que los divisores de 4 son 1, 2 y 4

D4={1,2,4}

Halla los divisores de:

D10= {

D8 = {

D15= {

CRITERIOS DE DIVISIBILIDAD

Los criterios de divisibilidad son reglas que permiten conocer cuando un número es divisible por otro.

4 de Junio

1. Escribe el conjunto de divisores de:

2. Fíjate en los ejemplos, piensa y completa el cuadro

29 de Junio

Números primos

Llamados también primos absolutos; son aquellos números mayores que 1 que tienen solo dos divisores, el mismo número y la unidad.

Los números primos son: 2; 3; 5; 7; 11; 13; 17; 19; . . .

Números compuestos

Son aquellos que no son primos es decir, son aquellos que poseen más de dos divisores.

Los números compuestos son: 4; 6; 8; 9; 10; 12; . . .

EXPERIENCIA PEDAGOGICA

Marca con un "X" el número según sea primo o compuesto.

Máximo común divisor

El máximo común divisor (mcd) de dos números es el mayor de la intersección de dos conjuntos de divisores.

EXPERIENCIA PEDAGOGICA

27 de Julio

Vamos a repasar las fracciones.

Representa gráficamente las siguientes fracciones. ( Escribir en el cuaderno y desarrollar)

EXPERIENCIA PEDAGOGICA (imprimir)

3 de Agosto

1. Represento las siguientes fracciones.

2. Representamos en el cuaderno las siguientes fracciones mediante gráficas y escribir si es propia o impropia:

¿QUÉ SON LAS FRACCIONES EQUIVALENTES?

Son aquellas fracciones que representan una misma cantidad, aunque el numerador y el denominador sean diferentes. Por ejemplo, tenemos dos tartas iguales. De una tarta nos comemos medio trozo y de la otra, nos comemos 2 cuartos de tarta, ¿en cuál de las dos queda más cantidad de tarta?

¡Efectivamente! Quedan en ambas tartas la misma cantidad. Aunque la primera la hayamos representado con un medio y la segunda con dos cuartos, las dos tartas representan la misma cantidad. Estas dos fracciones son equivalentes.

COMPLIFICACION (AMPLIFICACION) DE FRACCIONES

Es multiplicar el denominador y numerador de una fracción por un mismo número. Esta acción permite que tanto el denominador como el numerador de la fracción aumenten de valor tantas veces como veces se amplifica, pero el valor de la fracción como tal, se mantiene igual.

12 de Agosto

SIMPLIFICACION DE FRACCIONES

Dividir numerador y denominador por divisores comunes entre ambos hasta que no haya más divisores comunes.

EJEMPLO:

Escribe el siguiente ejercicio y practica.

EXPERIENCIA PEDAGÓGICA

19 de Agosto

COMPARACION DE FRACCIONES

26 de Agosto

EXPERIENCIA PEDAGOGICA

1.En una fiesta de cumpleaños le dieron 1/2 de torta a Juan y 1/4 a Carlos. ¿ A quién le dieron más torta?

Rta:

2. Francisco tiene 2/5 de empanada y Diego tiene 3/7 de empanada. ¿Quién tiene más cantidad de empanadas?

3. Escribe la fracción que representa la imagen y escribe el signo > o <.

Tarea

1. Hallar la fracción mayor o menor. > o <.

2. Realiza las sumas y las restas indicadas.

9 de Septiembre

SUMA Y RESTA DE FRACCIONES CON DIFERENTE DENOMINADOR

Para sumar o restar fracciones con diferente denominador, es decir fracciones heterogéneas se buscan fracciones equivalentes a las fracciones dadas, de manera que queden con igual denominador, y se efectúa la operación.

13 de Septiembre

23 de Septiembre

27 de Septiembre

NUMEROS DECIMALES

Los números decimales representa unidades completas (parte entera) y partes de la unidad (parte decimal).

En la parte decimal, es decir después de la coma va décimas, sigue centésimas y luego milésimas Cuando la parte entera es cero no se menciona.

Ejemplo: 0,2= dos decimas

0,08= ocho centésimas

0,045= cuarenta y cinco milésimas

7 de Octubre

SUMA Y RESTA DE DECIMALES

Para sumar y restar números decimales, se colocan un número debajo del otro, haciendo coincidir las cifras que son del mismo orden, es decir se coloca coma debajo de coma. Si la cantidad de cifras decimales no es igual se completa con ceros, se realiza la operación.